
 |
|
#161
|
|||
|
|||
|
Ahw. :/ I wonder if its possible to convert the figures to different altitudes..?
__________________
Il-2Bugtracker: Feature #200: Missing 100 octane subtypes of Bf 109E and Bf 110C http://www.il2bugtracker.com/issues/200 Il-2Bugtracker: Bug #415: Spitfire Mk I, Ia, and Mk II: Stability and Control http://www.il2bugtracker.com/issues/415 Kurfürst - Your resource site on Bf 109 performance! http://kurfurst.org 
|
|
#162
|
||||
|
||||
|
Good stuff IvanK, only thing that confuses me is the 'Merlin XX', i guess that's a typo of some sort, or was that some Mk.III testing?
Good information regarding Spitfire flaps down behaviour at page 11 of this document: http://ntrs.nasa.gov/archive/nasa/ca...1993092582.pdf
__________________
Bobika. |
|
#163
|
|||
|
|||
|
There is a Pencil Note on the first page next to the title "MKIII". This I presume is an annotation to indicate that the document is based on the spitfire MKIII which would also match the XX Merlin. A weird choice of variant to do tests with !
Got the NACA report. |
|
#164
|
||||
|
||||
|
Quote:
I am sure it does not say lower 85 degrees of flap and fly around in small circles. |
|
#165
|
|||
|
|||
|
Yes
|
|
#166
|
||||
|
||||
|
Quote:
V = TAS/SMOE = EAS Standard Means of Evaluation at 12,000 feet = 1.2011 Flaps up TAS at 12,000 feet = 160 mph TAS 160/1.2011 = 133 mph EAS 133 mph EAS * .869 = 115.6 KEAS Oh check it out....They give you EAS on the report. Gee, wasn't that another 100 page discussion on these forums? Anyway, once you have EAS you can easily convert the performance to any atmospheric condition you want. I like working with BGS but the units do not matter. Just don't put the correction factors like "1091" and "11.26" if you are using metric and keep your units straight. Our formula becomes: Radius = (VKeas * SMOE)^2 / 11.26tan <theta> <theta> = angle of bank which is a fixed relationship with load factor irregardless of altitude If you use the above formula and knots, our radius calculates out to be 693 feet and the RAE measurement is 695 feet. Pretty good agreement. Radius is not the primary turn characteristic in a fighter. It not so important how small the circle but how fast we can bring the nose around to put guns on target. So lets check our rate of turn based on the document: Flaps up = 160 TAS * .869 = 139 KTAS 1091(tan 68 ) / 139 KTAS = 19.42 degrees a second 360/19.42 = 18.56 seconds to complete a 360 degree turn 18.6 and 18.56 are a match.... Now let's see what it does at 20000 feet: 160 TAS at 12000 feet = 133 mph EAS 133 mph EAS * .869 = 115.6 KTAS SMOE @ 20000 feet from our Standard Atmospheric Data = 1.3700 Radius = (VKeas * SMOE)^2 / 11.26tan <theta> Radius = {115.6*1.3700}^2 / 11.26tan <68> = 899.97 or just 900 feet @ 20,000 feet Rate = 1091(tan 68 ) / (115.6KEAS*1.3700) = 17.05 degrees a second = 360/17.05 = 21 seconds to complete a 360 degree turn at 20,000 feet |
|
#167
|
|||
|
|||
|
Here are 3 Relevant Fan plots from the report posted without comment
Clean: 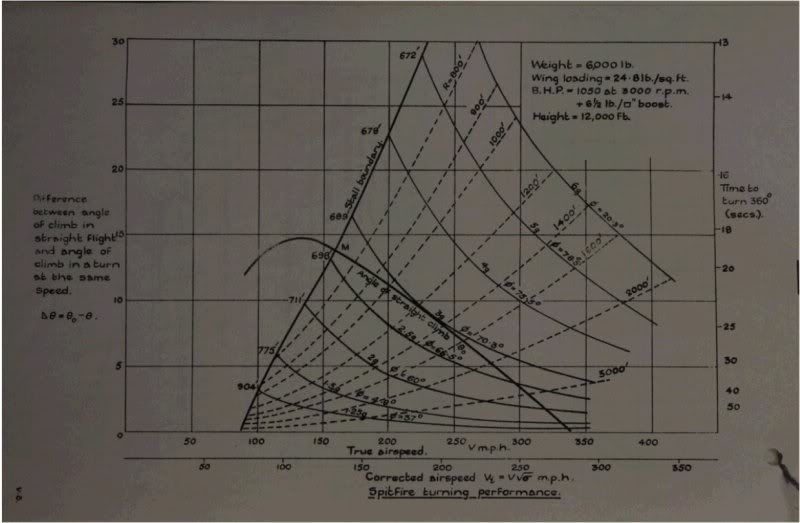 Flap 30 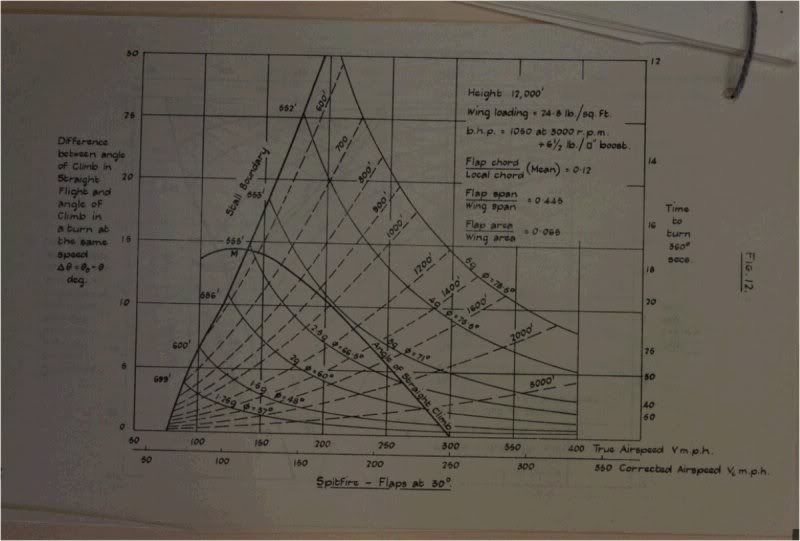 Flap 60 and Full at 85. 
|
|
#168
|
||||
|
||||
|
Quote:
It appears the RAE contradicts the NACA's findings on the effect of flaps on turn performance as well as what is taught in modern curriculum's. I really don't think that is the case and I bet that agreement is in the details of the report you posted. I understand your reluctance to share those details in this report. I would be happy to provide you the NACA findings on this subject. |
|
#169
|
|||
|
|||
|
Quote:
The way you simply use EAS above to derive results for 20,000 ft gives erroneous results that bear no relation to actual performance of the Spitfire at this altitude and a more realistic turn time under these conditions would be about 30 to 31 s. |
|
#170
|
||||
|
||||
|
Quote:
EAS is the most common expression for velocity in all aircraft performance calculation. It is the preferred expression because it is so simple to use. It is too easy to convert to TAS any performance derived with EAS and you don't have worry about density effects in the mechanics of the calculation. Just convert at the end. It also a great approximation of Indicated Airspeed and very easy to convert to that with a PEC chart and a universal compressibility.  Quote:
   If you are trying to quickly gauge relative performance you don't have to convert back to TAS. The specific numbers for rate and radius will change in proportion to density ratio which is a universal application. Last edited by Crumpp; 05-31-2012 at 09:34 PM. |
 |
|
|