Throwing some light on rates of turn

[MiG-3U]

Originally Posted by Crumpp

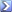
It is not hard to do at all. We can use the first entry for flaps up turn performance at 12000 feet.

V = TAS/SMOE = EAS

Standard Means of Evaluation at 12,000 feet = 1.2011

Flaps up TAS at 12,000 feet = 160 mph TAS

160/1.2011 = 133 mph EAS

133 mph EAS * .869 = 115.6 KEAS

Oh check it out....They give you EAS on the report. Gee, wasn't that another 100 page discussion on these forums?

Anyway, once you have EAS you can easily convert the performance to any atmospheric condition you want.

I like working with BGS but the units do not matter. Just don't put the correction factors like "1091" and "11.26" if you are using metric and keep your units straight.

Our formula becomes:

Radius = (VKeas * SMOE)^2 / 11.26tan <theta>

<theta> = angle of bank which is a fixed relationship with load factor irregardless of altitude

If you use the above formula and knots, our radius calculates out to be 693 feet and the RAE measurement is 695 feet. Pretty good agreement.


Radius is not the primary turn characteristic in a fighter. It not so important how small the circle but how fast we can bring the nose around to put guns on target.

So lets check our rate of turn based on the document:

Flaps up = 160 TAS * .869 = 139 KTAS

1091(tan 68 ) / 139 KTAS = 19.42 degrees a second

360/19.42 = 18.56 seconds to complete a 360 degree turn

18.6 and 18.56 are a match....

Now let's see what it does at 20000 feet:

160 TAS at 12000 feet = 133 mph EAS


133 mph EAS * .869 = 115.6 KTAS

SMOE @ 20000 feet from our Standard Atmospheric Data = 1.3700

Radius = (VKeas * SMOE)^2 / 11.26tan <theta>

Radius = {115.6*1.3700}^2 / 11.26tan <68>

= 899.97 or just 900 feet @ 20,000 feet

Rate = 1091(tan 68 ) / (115.6KEAS*1.3700)

= 17.05 degrees a second

= 360/17.05 = 21 seconds to complete a 360 degree turn at 20,000 feet

All you calculate here is the turn times at constant KEAS and constant g load (2.68 g which corresponds angle of bank 68 deg) at two altitudes, 12k and 20k. Then you claim that an airplane which can do this kind of sustained turn at 12k, can do sustained turn at same g load at 20k at same given KEAS. Note that your calculation does not account the engine power and the power might be different at 12k than at 20k.

Now, think this for a minute instead insult the other members of the board.