Merlin negative G cutout too quick?

[IvanK]

Sternjaeger you said:

"Anyway, back to the topic, the videos I have seen seem show quite a jolly response, but then again if it's on full throttle they are quite spot on. "

So let me get this right in your opinion an Engine cut with entry into a descent as shown in my video where G never gets lower than say +0.8G is enough to induce
engine cut ?

In a previous post you said: "A sustained 0G or a minimum negative G load (-0.1) are enough to interrupt the flow."
In this video we don't get any where near those values .

http://www.youtube.com/watch?v=Py7lf...layer_embedded

An engine cut at 0G or negative G value I wouldn't have an issue with. Here we are positive G throughout.

[Viper2000]

LONG POST ALERT
Those with limited tolerance for extended, somewhat generalised technical geekery should probably stop reading about now...

Originally Posted by Sternjaeger

Bloody norah! nother engineer!

my humble knowledge comes from a thing called experience (in this specific case experience with Merlin and other aviation engines), which is something you can't learn on a manual or at university, but for the sake of science (and in order to pass my exams) I also had my fair share of theory books..

Anyway, I meant on average going from the early marks to the late ones, but regardless of that, the comparisons that I've seen here are somewhat out of place. Comparing an air cooled boxer engine of a Cessna with a liquid cooled V12 is a bit of a silly thing, since the engine have humongous differences.

It's certainly not ideal, but in the absence of superior material, it's better than nothing.

Thermodynamically, the arrangement of the cylinders doesn't matter. Firing order does if you want to get into some kind of method of characteristics type modelling approach in the induction manifold in order to investigate scavenging etc., but this isn't really important to a discussion of negative g cut behaviour.

The size of the engine has in impact; bigger engines are closer to being adiabatic because the surface area:volume ratio is smaller so the heat transfer losses are less. This is important both inside the cylinders and inside the intake manifold (especially if fuel is not injected directly into the cylinders).

For our purposes, the main impact of engine size is that the Merlin's induction manifold is nice and neat, and would probably give better mixture distribution than is possible for GA boxer engines.

But really, induction manifold scale effects are going to be very much second order.

The main point of interest is the carburettor itself. The main scale effects of interest will be those associated with the float chamber.

Reynolds number scales with linear dimension, whilst one might reasonably assume that float chamber volume would scale approximately with power, and thus float chamber linear dimension would scale with power^(1/3).

So if we assume that the Merlin II and III had carburettors sized for about 1100 bhp, whilst the GA boxer engine is sized for about 110 bhp (ie Cessna 152 powerplant) then the characteristic Reynolds numbers determining the behaviour of the fluid flows within the carburettor will only differ by about a factor of 10^(1/3) which is about 2.15.

Without making reference to design drawings or going into a relatively deep analysis, it's quite difficult to say whether this Reynolds number difference will dramatically affect the flow.

However, I would observe that the chances are that the flow is turbulent in both cases, and therefore my gut feeling is that the qualitative differences in flow phenomena should be relatively small. This is supported by the fact that people have built and run much smaller piston engines without needing to radically alter their carburettor design. Indeed, there's even a very nice scale Merlin out there somewhere:

http://www.youtube.com/watch?v=0xe1LL1IC7Y

What is more likely to be significant is that the larger physical size and mass of the moving components in the Merlin's carburettor will make it easier for inertial loads to defeat stiction.

So a computer model of a Merlin assuming zero friction in carburettor moving parts would be closer to reality than one of a smaller engine.

However, the fact that the smaller carburettors work would tend to imply that the "controlling" forces still tend to dominate. Naturally, the vibration of the engine will tend to help the smaller carburettor to overcome stiction (which is of course the engineering justification for the price of an aerotow being set by the reading on the tug pilot's altimeter; but I digress).

Therefore, the implication is that the biggest difference will be that the Merlin's carburettor float will be less well damped than that of a smaller engine.

My judgement based upon this argument is that a pair of photographically scaled carburettors sized for the order of 100 bhp and the order of 1000 bhp should behave in a similar manner when subjected to reduced or negative g for sufficient time that oscillation of the float is damped. This is not to suggest that their behaviour will be identical; what I'm saying is that they should misbehave at roughly the same g loading.

This sort of simple argument from first principles is far from the ideal way to approach the problem; but I don't have any alternative available to me at present, so it will have to do.

Originally Posted by Sternjaeger

As for the Merlin not being a delicate engine, I beg to differ, and seriously too. The most delicate part of the Merlin is actually the cylinder banks, where -because of the external cooling jacket - cracks and microcracks are hard to spot unless going with internal inspection. A radial engine can still fly with a damaged piston and/or cylinder, a Merlin simply can't. Damages to cylinder banks on Merlins are normally the reason why we have engine failures still today. You have to appreciate that the planes we have today use 60+ years old banks, not to mention that some pilots today still think you need 100% throttle for takeoff, while we normally takeoff at 75% to save on engine life and play it safe (and because there's SO much power!). Another cause of cracks is not paying attention to temperatures, which can cause further thermal fatigue to the banks, especially on a cold start.

Well yes; I don't think anybody expected Merlins to still be flying 70+ years after the first one came off the line. It's hardly surprising that really really old banks are somewhat delicate.

When I say that the Merlin is a relatively tough engine, what I mean is that you can actually go through the RRHT books and see the records of endurance running at high power, which will show you that in general, by the time a rating was signed off, the engine for which it was approved could probably run at that sort of power for a very extended period (100 hours+) continuously, without maintenance, and not break.

You can see how strong the basic engine is by looking at how hard they push them at Reno (albeit with various mods like V-1710 con rods etc) whilst still reasonably expecting to get through a race distance without failure. It's quite hard to get accurate data because naturally the teams are secretive, but they're probably at least +36 psi/3200 rpm for around 2600 bhp plus exhaust thrust. Which isn't bad for a machine originally designed for an international rating of roughly 1000 bhp. It's particularly impressive that the reduction gears stand up to it...

Of course, the early engines that we're dealing with in CoD were rather less robust than the later ones because they hadn't been subjected to such intensive development.

Cooling leaks were a continual problem, and were one of the main motivations for switching from pure glycol to 70% water 30% glycol. Of course, this is often spun in less intelligent history books as "allowing engine temperatures to be reduced by 70º C, greatly improving reliability", but what it really means is that the reliability was poor, so lowered the coolant temperature and accepted the drag penalty of bigger radiators rejecting heat at lower temperature, greatly reducing the scope for exploiting the Meredith effect (i.e. running the radiator as a low temperature ramjet; a peak cycle temperature of 393 K rejecting to about 250 K gives much less useful work potential than 463 K rejecting to 250 K).

Originally Posted by Sternjaeger

The G loads don't affect only the carburetor btw, but the inlet manifolds as well, so cutouts can be more or less abrupt. I haven't had the chance to fly the sim yet, maybe a video would help understanding better.

You'd hope that the stuff going through the intake manifold was hot air plus gaseous fuel, so you've got a mixture with a reasonably low density (<2 kg/m^3 for an early engine below FTH). This is going to be far less susceptible to the effects of g loading than liquid fuel of density c.720 kg/m^3.

The g is more likely to have an impact upon the intake manifold during the rich cut if droplets of liquid fuel persist downstream of the supercharger, but since we know that the initial cut is a lean cut rather than a rich cut, it seems reasonable to relegate this to the status of a second order effect.

There might be a bigger impact for a naturally aspirated engine, because they tend to be much less good at mixture distribution, and can suffer from liquid fuel pooling around in their induction manifolds. Obviously this liquid fuel will tend to mitigate any lean cut caused by misbehaviour of the carburettor.

Originally Posted by Sternjaeger

gosh, I would spend hours at the pub (or at the hangar with a pint) talking about this stuff mate lol

You're on.

Originally Posted by Sternjaeger

IvanK it's no guesswork, you need a G-meter to determine it properly. A sustained 0G or a minimum negative G load (-0.1) are enough to interrupt the flow. Despite what our scientist friends here say, the mixture gets to the cylinder inlet almost instantaneously. As you know it's not like cylinders burn mixture all at the same time, so one cylinder not receiving enough mixture for a full detonation is enough for a cutout sometimes. Again, please guys provide me with a video and I will be able to tell you (in my humble opinion) if the effect is overmodelled or not.

Sustained zero g means that the position of the float is undefined. This means that if the system would work at small positive g, then it should keep working at zero g because a body at rest remains so until disturbed by an outside force or influence.

OTOH, small negative g redefines the system "upside down", and so misbehaviour should result as soon as that negative g becomes sufficient to overcome stiction.

However, it's not immediately obvious to me that the system should work at small positive. "Modern" GA piston engines seem happy enough for a few seconds at zero, but unhappy under small negative g, which would tend to support this model.

But OTOH, the video of the Hurricane flying in The Battle of Britain film intro I posted earlier looks more like reduced positive than genuine negative to me, and AP2095 posted by IvanK imply that there might be trouble at +0.5 g.

So I don't know. It's quite possible that even the humble GA piston engine has benefited from WWII experience and now has a zero g capability not found in the first generation Merlins. Or it could be that the Hurricane in that video I posted actually did push into negative (in which case it was a pretty bad barrel roll...).

My approach to the problem needs more information in order to proceed, specifically, design drawings or cutaway drawings of both the original Merlin SU carburettor on the one hand, and of a representative carburettor fitted to a modern GA engine on the other, so that we can then decide whether or not, based upon the logic I have outlined above, the GA carburettor's reduced and negative g behaviour might be expected to be broadly similar to that of the Merlin's SU or not.

As for the characteristic time for an engine cutout we can say several things.

The volumetric flow capacity of the Merlin flat out is roughly

27 litres * 3000 rpm/120 litres per second = 675 l/s.

For the sake of argument, let's consider a Merlin II at about 17000 feet and +6.25 psi boost.

We can assume that the supercharger has an isentropic efficiency of something like 67%. Ambient pressure is about 52.7 kPa and ambient temperature is about 254 K. We shall neglect intake ram effect because life's too short.

+6.25 psi boost = 20.95 psi absolute ~ 144.4 kPa

Supercharger pressure ratio is therefore 2.74.

Isentropic temperature ratio is therefore 2.74^(0.4/1.4) ~ 1.33

Isentropic delivery temperature is therefore 338 K. Delta T is therefore about 85 K (I just rounded up). Assuming constant Cp, which isn't unreasonable for this sort of temperature in a back of envelope calculation, this means that the real temperature rise is

85 K/0.67 ~ 125 K

The absolute delivery temperature is therefore about 379 K.

We want to know the density at compressor delivery. Since I'm not about to break out the really heavy computational firepower to do this properly, the simplest way I can think of doing this is to treat the real compression process as 2 processes, namely, isentropic compression and constant pressure heat addition.

So the isentropic delivery was 338 K and 144400 Pa.

From the ideal gas law we know that V2/V1 = (P2/P1)^(-1/gamma)

Ambient density is 0.72209 kg/m^3 at 17000' on a standard day.

Specific volume is 1/roh, therefore V1 = 1.385 m^3/kg. Thus V2 = 0.674 m^3/kg and therefore roh2 is 1.483 kg/m^3.

Now we add heat at constant pressure;

V3/V2 = T3/T2 = 338/379

Therefore

roh3/roh2 = 379/338 = 0.892

Thus roh3 = 0.892*1.483 kg/m^3 = 1.323 kg/m^3.

(So we actually haven't won a great deal compared with standard sea level density, but at least we're getting it at 17000'...)

Since we already know that the volume flow rate is 675 l/s, we now know that the mass flow rate is about 0.893 kg/s, which gives an hourly air consumption of about 3214.5 kg.

Cross-check with the known fuel flow - 89 imperial gallons is about 404.6 litres, so at specific gravity 0.72 it has a mass of about 291.3 kg.

Therefore the FAR is about 0.09, for an air:fuel ratio of 11:1, which is pretty much bang on given that we'd expect to be considerably rich of peak.

This separation of air and fuel is based upon the assumption that the fuel is very much denser than the air, and that most of the mixing takes place in the supercharger and intake manifold. It's rather quick and dirty stuff because IRL you'd get about 25 K temperature reduction from fuel evaporation, but then if you start accounting that the compression process isn't really adiabatic anymore and the whole thing becomes too much like real work...

We now have a reasonable idea of what's going on in the intake manifold.

The next stage is to consider how long it takes for a change in FAR to impact the engine.

The induction manifold is about 2 m long. Given dimensions we can work out the approximate steady flow Mach number needed to pass the calculated total mass flow, and hence the time taken for the charge to reach the last cylinder.

From these pictures we can infer that the intake manifold is about 3" internal diameter, which for the sake of argument we might as well call 7.5 cm. So the area is about 0.0044m^2.

Since the volume flow rate has already been defined as 0.675 m^3/s, the steady flow velocity down the pipe must be about 153 m/s, which is around Mach 0.4, which is within the realms of reasonable expectation.

The time to deliver charge along the manifold is about 1/75th of a second; say 1/150th of a second for the average cylinder.

The engine is turning at 3000 rpm. There are therefore (1500*12)/60 = 300 induction strokes per second.

So the time taken for the charge to travel along the induction manifold is somewhat longer than the interval between induction strokes for all but the rearmost cylinders.

Whilst 1/75th of a second may sound like a very short interval, it's worth pointing out that a lot of people will be aiming for that sort of framerate once the sim is patched & they've bought their shiny new upgrade hardware; and that's before we even consider the possibility of multiple FM frames per visual frame (which is a technique used in at least one other sim, i.e. X-Plane).

So, just as we have an animation showing individual exhaust pulses, it wouldn't be unreasonable to model this sort of time delay between the mixture starting to lean out at the carburettor and the FAR seen by the engine starting to lean.

However, it is likely that the longest lag in the system will be associated with the carburettor itself, which is not the sort of thing I'm equipped to analyse; as a thermodynamicist, I'm not not really a master of the dark arts that are the fluid mechanics of multi-phase flows.

(Ok, so quite a lot of the thermodynamics wasn't really necessary, because I guess I could have just inferred the induction manifold speed from the dimensions and the volume flow rate, but I was distracted so I hit it with an excessively large computational hammer; it seems a shame to delete it all, now, so I've just left it in for the amusement/horror of the assembled company).

Originally Posted by TheGrunch

It's probably worth pointing out that Sternjaeger will never have experienced the Merlin engine at combat power or indeed emergency boost because unfortunately (or perhaps very fortunately, we don't want to destroy every Merlin on the planet ) no one does that anymore for practical reasons...this being the condition at which the cut-out is least severe in its onset.

They push them much harder than emergency boost at Reno...

http://www.youtube.com/watch?v=iBqpn9VXek8

You can even see how much power they pull for takeoff and the run in; but unfortunately the race power settings are censored.

However, 2800/55" Hg for 257 IAS/318 TAS should tell you that he's not exactly sparing the horses during the racing laps, given that power required is roughly proportional to v^3.

Very roughly, if 2800/55" is 1500 bhp, and that's giving 318 mph TAS then the race power to average 440 mph TAS would be about 3900 bhp.

The highest power cleared for ground running during WWII was about 2600 bhp, achieved by the RM17SM engine at 3100 rpm, +36 psi with ADI.

Of course, the Reno guys will never see a negative g cut, but that's not because they coddle their engines!

Originally Posted by Sternjaeger

I have experienced 100% throttle but not on take-off. It's highly not recommended to use full military power or 100% throttle anyway, again because of the components age concern.

I believe that in most fighters the recommended takeoff power was about +12/3000, which will give around 1200 bhp depending upon MS gear ratio, which should be more than enough given a sensible runway and no war load.

I would have though that in general it would be safer to use less power in order to mitigate the handling issues, because most people wouldn't try to operate their extremely expensive warbird out of a length limited airfield.

Originally Posted by Sternjaeger

A very quick but effective way to check the health of your engine is checking the lubricant oil for metal particles: they can be microscopic, but if found (often by means of special filters) they're a bad, bad sign.

There was a certain P-51 driver a couple of years ago who had the jolly habit to take off firewalling the throttle: needless to say the cylinder banks didn't want to know about it and an inflight engine failure followed, which fortunately happened close to landing.. the plane and pilot were ok, but the engine needed major (expensive) maintenance costs. Let's not forget that like any other liquid cooled engined, these monsters were meant to perform, not to last

That's a whole lot of horses:

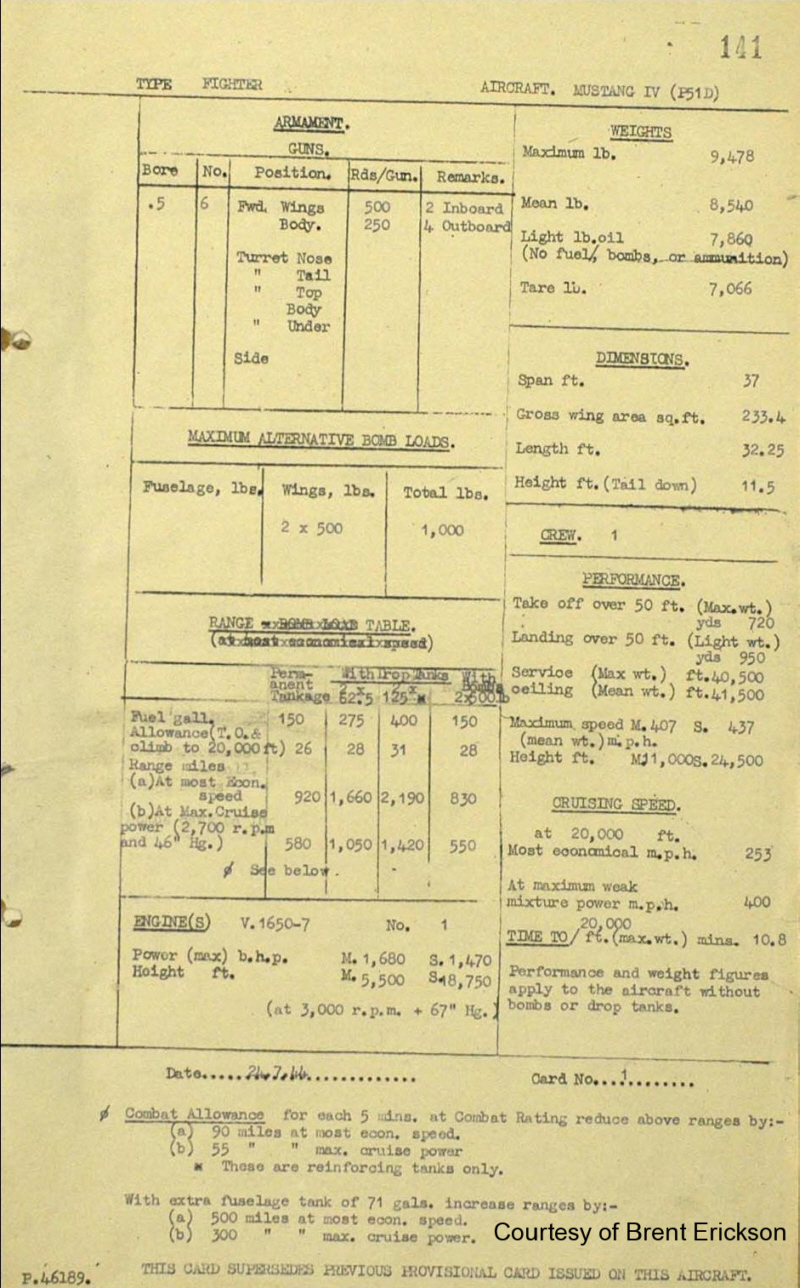And even the wartime manual suggests that full chat isn't a good idea for takeoff...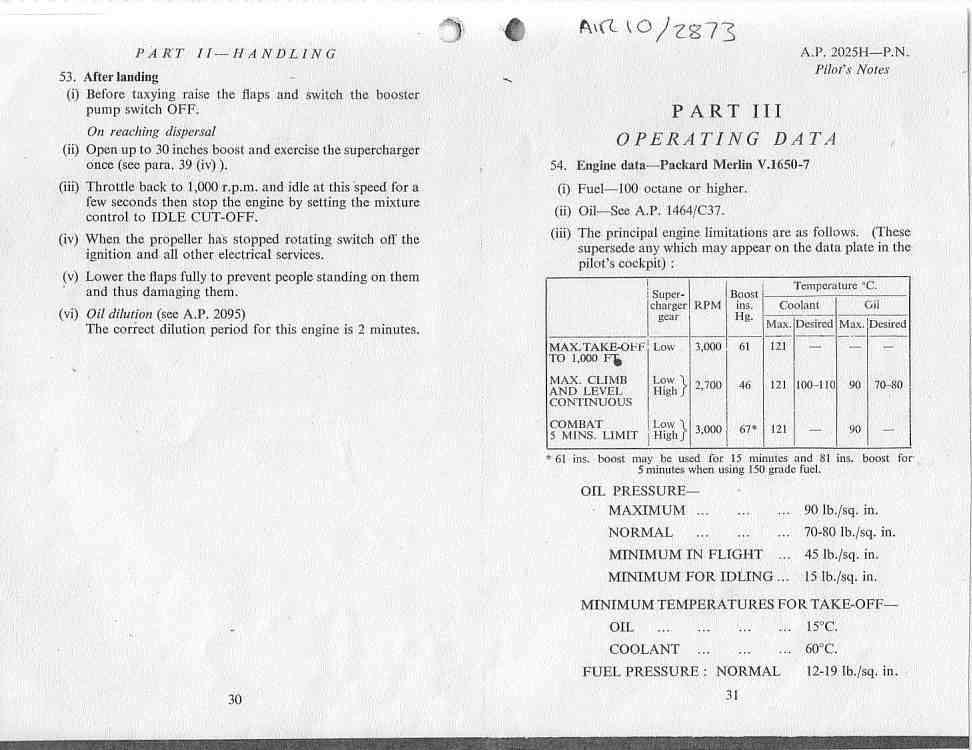


I suppose this is another example of the sad fact that many people have more money than sense; I mean, if I was going to fly a Mustang at high power, I'd wait until it was going fast to start bending the throttle in order to maximise the benefit and minimise the cooling and handling worries.

Originally Posted by Sternjaeger

btw, I forgot to tell that my flying experience isn't with early Merlins, so de facto I have never had a cut out with the Merlin. I had it with other gravity fed machines (I once had a very hair raising experience with a Tiggie which left me falling down like a leaf with a dead engine..), but I asked one of the engineers this afternoon and he said that yes, power loss and cut out would be quite abrupt. As you probably know negative G or inverted flight is not recommended on a Merlin anyway because of its lubrication system configuration: you'd have oil coming up and messing up the cylinders and leaving the crankshaft dry. Another advantage that the DB engine had over the Merlin apparently.

A.

Most engines don't like extended inverted running; generally the limit is less than about 30 seconds of sustained negative g unless the engine & fuel system are specially designed for the job (i.e. in a dedicated aerobatics machine).

Originally Posted by Sternjaeger

regarding the needle bounce I think it's overmodelled. RPM gauges are connected by flex cable to a reduced gearbox attached on a specific slot on the back of the engine, so they're as accurate as it gets. You can get high frequency vibrations, but oscillations like that means that either your instrument is fooked or your engine is actually doing those oscillating RPM peaks (which is weird..).

+1. I can't really think how the bounce could be that bad unless something was broken, especially since you can rule out a bad CSU in the case of the Spitfire I with its 2 position prop, implying that either there's continual engine rpm variation or an awful instrumentation problem...

The other possibility is that the prop mass is out by an order of magnitude and there therefore is far too little angular momentum in the system to smooth out engine rpm variations. It just depends on how complex the underlying model really is I suppose...

[/procrastination] (though actually this little lot was mostly written whilst waiting for code to run; which of course is why it's ended up getting so massive; the real procrastination has been tidying it up at the end...)

[IvanK]

Fascinating post thanks for the effort in writing it.

[Deadstick]

@Viper 2000, I am both amused and horrified. Thank you for the post.

Originally Posted by Deadstick

@Viper 2000, I am both amused and horrified. Thank you for the post.

+1

Viper, you need to get out more mate, think about all the hot birds you could have met at uni whilst the code was running

on a serious note, yes, your calculations are somewhat interesting (if I can suggest something, try and keep it simpler..), but not conclusive

two things though:

a) don't take Reno Racers into account, those folks really have more money than sense and 1) have custom built cylinder cases, pistons, piston rods, valves and modified superchargers (their special mixtures+the very low altitude means that the mixture gets VERY hot, and the intercooler of the two stages supercharger can struggle to keep things to the right temperature - the rule of thumb with Reno Racers is "don't believe in what they say, they play a lot on the "secrecy" thing..") 2) run on "special" fuels. It's fascinating but somehow appalling to see them do what they do with those machines..

b) not always warbirds owners fly their own planes. And when you're a pilot who's flying a £2mln warbird that doesn't actually belong to you, you might get a tad too jolly on it.. another important thing to take into account for modern warbirds is that most of the heavy stuff (old radios/batteries, central fuel tank, armour, ammunition and armament) is gone, a slimming process that makes the thing sensibly better in terms of perfomance.

[IvanK]

Repost of post 41 for your comment Sternjager:

Sternjaeger you said:

"Anyway, back to the topic, the videos I have seen seem show quite a jolly response, but then again if it's on full throttle they are quite spot on. "

So let me get this right in your opinion an Engine cut with entry into a descent as shown in my video where G never gets lower than say +0.8G is enough to induce
engine cut ?

In a previous post you said: "A sustained 0G or a minimum negative G load (-0.1) are enough to interrupt the flow."
In this video we don't get any where near those values .

An engine cut at 0G or negative G value I wouldn't have an issue with. Here we are positive G throughout.

Originally Posted by IvanK

Repost of post 41 for your comment Sternjager:

Sternjaeger you said:

"Anyway, back to the topic, the videos I have seen seem show quite a jolly response, but then again if it's on full throttle they are quite spot on. "

So let me get this right in your opinion an Engine cut with entry into a descent as shown in my video where G never gets lower than say +0.8G is enough to induce
engine cut ?

In a previous post you said: "A sustained 0G or a minimum negative G load (-0.1) are enough to interrupt the flow."
In this video we don't get any where near those values .

An engine cut at 0G or negative G value I wouldn't have an issue with. Here we are positive G throughout.

if you never get lower than +0.8G then no, it's not correct, but you need to be sure of the G-load value mate.

just had a word with one of the pilots, who confirmed me that as soon as you hit 0G with a float carburettor it's enough for the engine to falter or cut. He said the Harvard does it regularly (I never experienced stalls or 0G manouvres with it so I couldn't tell personally).

[IvanK]

Ok thanks for that, then based on that 0G is significant. If we accept 0G as the point at which the coughing starts then what we have now is GROSSLY over done.


I have a pretty good idea of 0G and the pitch rates required to achieve it in high performance aeroplanes and we are getting nowhere near it in COD before the engine starts coughing.

[Seeker]

It does seem very strange to me that the Merlin installation, lacking fuel injection as it was, though intended for an aerobatic use, is less robust to negative G than either a Prewar Matchless scrambler or the pilot's MG TA.

I can keep an MG TA for negative G for about2 to 3 seconds without it cutting out. The lube system is much more sensitive than the carbs, as merely throwing it hard into a roundabout can get the oil thrown to one side of the sump, but while I've heard bearing knock on round abouts and good hump back bridges, it's never had metering problems.

Of course it's a completely spurious comparison, but nonetheless odd that a machine designed for 2 D is more robust in this matter than a machine designed for 3D.